Poiseuille flow is pressure-induced flow ( Channel Flow) in a long duct, usually a pipe. It is distinguished from drag-induced flow such as Couette Flow. Specifically, it is assumed that there is Laminar Flow of an incompressible Newtonian Fluid of viscosity η) induced by a constant positive pressure difference or pressure drop Δp in a pipe of length L and radius R << L. By a pipe is meant a right circular cylindrical duct that is a duct with a circular crosssection normal to its axis or generator.
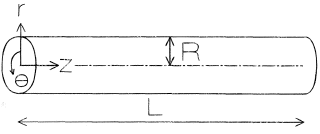
Because of the geometry, Poiseuille flow is analyzed using cylindrical polar coordinates (r, θ, z) with origin on the center-line of the pipe entrance and z-direction aligned with the center-line (see Figure 1). Symmetry means that Poiseuille flow is swirl-free and axisymmetric. Thus, the only nonzero components of the velocity u are the radial component ur and the axial component uz: the angular component uθ = 0. Moreover, ur and uz are independent of θ, as is the pressure p. Because the pipe is long, Poiseuille flow is fully developed, that is the velocity u is independent of axial position z everywhere except near the entrance (z = 0) and exit (z = L) of the pipe, from which it follows that ur = 0. Solution of the mass and linear momentum conservation equations, specifically the Navier-Stokes equations, with boundary conditions of no-slip at the pipe wall (r = R) and symmetry at the center-line (r = 0) yields [see Richardson (1989)]

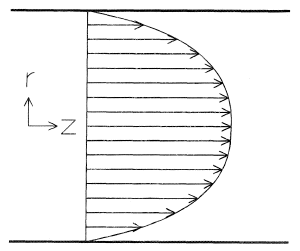
Thus the axial velocity profile is parabolic (see Figure 2). The maximum axial velocity urmax occurs at the center-line (r = 0) and is given by

whereas the mean axial velocity ūz is given by

from which it follows that ūz = urmax/2 . The volumetric flow rate  through the pipe is given by
through the pipe is given by

This is the Hagen-Poiseuille Equation, also known as Poiseuille's Law. Experimentally, Eq. (4) is found to be corroborated provided the Reynolds Number (Re) given by

is less than some critical value Rec = 2000, so that there is laminar flow and not Turbulent Flow, though it should be noted that Rec appears to be very much larger than 2000 if particular care is taken to minimize disturbances which might cause flow instabilities; and provided L/R >> C Re where C ~ 0.1, so that the pipe is long enough for entrance and exit effects to be negligible and hence for u to be fully-developed.
Poiseuille flow is a shear flow with shear-rate γ given by

The viscous dissipation rateε is given by

Dissipation of mechanical energy, that is conversion of mechanical energy (specifically pressure energy) into thermal energy by viscous action, increases the temperature T of the fluid. Assuming, that the temperature T is fully developed, the solution of the energy conservation equation with boundary conditions of specified temperature Tw at the pipe wall (r = R) and symmetry at the center-line (r = 0) yields [see Richardson (1989)]

where λ denotes thermal conductivity. Experimentally, (8) is found to be corroborated provided L/R >> C Pe where C ~ 0.1 and the Peclet Number (Pe) is given by
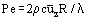
where c denotes specific heat. The pipe is then long enough for entrance and exit effects to be negligible and hence for T to be fully-developed.
For Poiseuille flow in channels or ducts of noncircular crosssection, analogous expressions can be obtained for velocity and temperature [see Happel and Brenner (1973) and Shah and London (1978)].
REFERENCES
Happel, J. and Brenner, H. (1973) Low Reynolds Number Hydrodynamics, Noordhoff, Leyden.
Richardson, S. M. (1989) Fluid Mechanics, Hemisphere, New York.
Shah, R. K. and London, A. L. (1978) Laminar flow forced convection in ducts. Advances in Heat Transfer, Supplement 1, Academic Press, New York.
References
- Happel, J. and Brenner, H. (1973) Low Reynolds Number Hydrodynamics, Noordhoff, Leyden.
- Richardson, S. M. (1989) Fluid Mechanics, Hemisphere, New York.
- Shah, R. K. and London, A. L. (1978) Laminar flow forced convection in ducts. Advances in Heat Transfer, Supplement 1, Academic Press, New York.