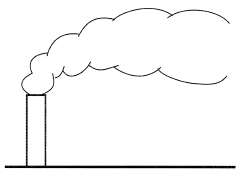
Gas or aerosol released into the atmosphere at an approximately steady rate, for example, from a chimney, will advect with the wind and take on an elongated shape reminiscent of a large feather (Figure 1). Such a cloud is known as a "plume". Plumes arise in a variety of circumstances, the essential features being the existence of a continuous, finite sized source of material and a preferential flow direction, which elongates the cloud. The term is applied equally to underwater liquid releases, and although this article concentrates on atmospheric plumes the general principles are the same in the underwater case.
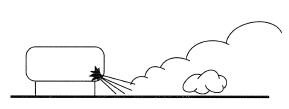
Sources of plumes in the atmosphere include discharges from a chimney, fires, and blow-down of a pressurized vessel (Figure 2) or pipe work through an accidental puncture. A number of features may introduce a preferential flow direction: the direction of the ambient wind; intrinsic momentum generated in a release from pressure; and buoyancy forces. A plume with high intrinsic momentum is a "jet" (in which the velocity decreases as one goes down stream) until a point is reached where the other factors dominate the directional flow. The term "plume" is sometimes used specifically for cases where these other mechanisms are dominant.
The simplest case is that of a steady plume, where discharge from a constant source has been occurring for long enough that the plume is well developed over the relevant range downstream from the source. In this case there is a conserved flux of the material emitted from the source. This is related to the principal plume variables by

where S(x) is an appropriate measure of the cross-sectional area at a distance x along the plume center line from the source, c is a measure of the concentration, and u is a measure of the plume velocity. In different models c and u may be cross-sectional averages or, if self-similar profiles of concentration and velocity are assumed, center line values. As one goes downstream, air is mixed into the plume causing the concentration to decrease and the area to increase. For plumes adverting with the wind, u(x) may be fairly constant or increase if the plume rises; for jets u(x) decreases dramatically.
The rate of mixing depends on the level of turbulence present. Turbulence is generated by the wind (atmospheric shear flow) and also by shear in any other fluid motion associated with the plume including buoyancy-driven flow or jet flow. In different situations, different turbulence generation mechanisms may dominate the mixing process; the most complex cases are where no single turbulence generation mechanism dominates, (see also Turbulence).
The above definition of a steady plume makes some implicit assumptions about atmospheric turbulence. In particular, that it is possible to define a concentration averaged over a sufficiently long time to even out fluctuations due to plume meander, but sufficiently short to make the idea of a fixed wind direction meaningful. Looking at visible plumes from chimneys, this assumption is intuitively plausible, but often requires careful consideration when applying the analysis to specific situations.
Perhaps the classic example of a steady plume description is the Gaussian model of a plume adverting horizontally with the wind at a height h. In this case mixing is purely due to atmospheric turbulence, and the concentration is assumed to have a self-similar Gaussian profile

The conserved flux is as given above with S(x) = 2πσy(x)σz(x) and u is the constant wind speed at height h. The parameters σy(x) and σz(x) are assigned empirical forms dependent upon atmospheric stability, which is usually quoted in terms of a Pasquill category (also empirical) in the range A to F or G, see, for example, Hanna and Drivas (1987), Panofsky and Button (1984). This model is simple but adequate for many purposes. It is often elaborated to allow for the presence of the ground (to ensure that the entire flux of material remains above the ground).
Such a model can be used to describe a passive plume. "Passive" means that the local flow is unaffected by the presence of the plume, which must have no buoyancy or momentum. It is not appropriate for dense or buoyant plumes, except in the very far field when dilution will eventually render either of these passive.
In discharges from chimneys, buoyancy is often an aid to getting the plume as high as possible into the atmosphere and enhancing dilution. Plumes from fires are also buoyant, and the plume rise may mitigate the immediate consequences of toxic combustion products, although not necessarily the long term environmental impact. In the absence of wind, or where the speed of rise is much more rapid than the wind speed, such a plume will rise vertically. Its buoyancy determines its rate of rise, which in turn determines the level of turbulence, which induces mixing which dilutes the plume and reduces the buoyancy. Turner (1973) gives a clear analysis of this situation. Any variation in atmospheric density with height will also affect the behavior of the plume.
If there is a wind then the plume will bend over. The trajectory and turbulent dilution rates are affected both by the wind flow and by buoyancy, as well as by atmospheric stratification and any momentum at the source. Simple analyses, similar to the vertical plume rise case, may apply in some cases where the buoyancy-generated turbulence dominates atmospheric turbulence, as discussed by Hanna, Briggs, and Hosker (1982). Relatively simple descriptions are also applicable to momentum-dominated plumes (Jets).
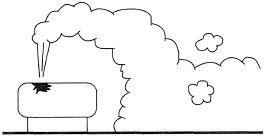
However, the general case of a (positively or negatively) buoyant airborne plume, possibly with initial momentum, in a turbulent atmosphere is more complicated. For example, a dense jet may be emitted upwards and, as it loses momentum and becomes dominated by buoyancy forces return back to the ground (Figure 3), or it may dilute to the extent that it becomes passive while still airborne.
Dense plumes at ground level are often the expected result of accidents to chemical plant. Many substances may form dense clouds owing to high molecular weight, low temperature, or liquid aerosol content. (For example, ammonia and LNG readily form heavy clouds despite having low molecular weight.) Such plumes have received much attention as the danger associated with them is enhanced by their density: they stay close to the ground and dilute more slowly as any mixing must overcome the stable density interface at the top of the cloud. (Although very close to the source mixing may be enhanced by turbulence generated from the slumping behavior of the cloud.) The main parameter which affects the mixing rate is the Richardson Number—typically Ri = g(ρ ~ ρa)H/(ρa ) for a cloud of height H and density ρ in an atmosphere of density ρa in which the velocity associated with turbulence is characterised by u*. Thus a large cloud in a still atmosphere may be effectively dense, even if its density is only very slightly greater than that of the ambient air. The width of a ground-based dense plume may increase much more rapidly than the passive case as the plume slumps. Correspondingly the height increases more slowly or may even decrease for a limited distance downstream. Wheatley and Webber (1984) and Britter and McQuaid (1988) discuss heavy clouds in detail.
) for a cloud of height H and density ρ in an atmosphere of density ρa in which the velocity associated with turbulence is characterised by u*. Thus a large cloud in a still atmosphere may be effectively dense, even if its density is only very slightly greater than that of the ambient air. The width of a ground-based dense plume may increase much more rapidly than the passive case as the plume slumps. Correspondingly the height increases more slowly or may even decrease for a limited distance downstream. Wheatley and Webber (1984) and Britter and McQuaid (1988) discuss heavy clouds in detail.
REFERENCES
Britter, R. E. and McQuaid, J. (1988) Workbook on the dispersion of dense gases, UK Health and Safety Executive Report 17/1988.
Hanna, S. R., Briggs, G. A., and Hosker, R. P. (1982) Handbook on Atmospheric Diffusion, Technical Information Center of the U.S. Department of Energy DOE/TIC-11223.
Hanna, S. R. and Drivas, P. J. (1987) Vapour Cloud Dispersion Models, American Institute of Chemical Engineers, ISBN 0-8169-0403-0.
Panofsky, H. A. and Dutton, J. A. (1984) Atmospheric Turbulence, John Wiley and Sons, ISBN 0-471-05714-2.
Turner, J. S. (1973) Buoyancy Effects in Fluids, Cambridge University Press, ISBN 0 521 08623 X.
Wheatley, C. J. and Webber, D. M. (1984) Aspects of the dispersion of denser-than-air vapours relevant to gas cloud explosions, Commission of the European Communities EUR 9592, ISBN 92-825-4712-4.
References
- Britter, R. E. and McQuaid, J. (1988) Workbook on the dispersion of dense gases, UK Health and Safety Executive Report 17/1988.
- Hanna, S. R., Briggs, G. A., and Hosker, R. P. (1982) Handbook on Atmospheric Diffusion, Technical Information Center of the U.S. Department of Energy DOE/TIC-11223.
- Hanna, S. R. and Drivas, P. J. (1987) Vapour Cloud Dispersion Models, American Institute of Chemical Engineers, ISBN 0-8169-0403-0.
- Panofsky, H. A. and Dutton, J. A. (1984) Atmospheric Turbulence, John Wiley and Sons, ISBN 0-471-05714-2.
- Turner, J. S. (1973) Buoyancy Effects in Fluids, Cambridge University Press, ISBN 0 521 08623 X.
- Wheatley, C. J. and Webber, D. M. (1984) Aspects of the dispersion of denser-than-air vapours relevant to gas cloud explosions, Commission of the European Communities EUR 9592, ISBN 92-825-4712-4.