A perfect gas is a gas, which follows the equation of state:

where p denotes the pressure (N/m2); 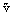 the molar volume (m3/mole);
the molar volume (m3/mole);  (= 8314 J/mole K or 8314 kJ/kmole K) the universal gas constant; and T absolute temperature, K.
(= 8314 J/mole K or 8314 kJ/kmole K) the universal gas constant; and T absolute temperature, K.
If both sides of the equation are divided by  (the molecular mass of a given gas), the equation will be:
(the molecular mass of a given gas), the equation will be:

where v denotes the specific volume (m3/kg) and R the gas constant for the gas under consideration (J/kg K).
From the equation of state and from the equations of thermodynamics differentials

it can be shown that ( ) = 0, i.e. the internal energy of the perfect gas does not depend on volume; this may be regarded as an independent property of a perfect gas.
) = 0, i.e. the internal energy of the perfect gas does not depend on volume; this may be regarded as an independent property of a perfect gas.
Often it is assumed that at p → 0, and at any temperature T, every real gas becomes identical to perfect gas. However, this is not necessarily true.
At moderate pressures as a theoretically proved equation of state for a real gas is the virial equation as follows:

where B, C … are respectively the second, third etc. virial coefficients, which are only temperature dependent. This equation can be rearranged as follows:

where the primed coefficients B’, C’, etc. are also functions only of the temperature and can be expressed in terms of B, C … .
For instance

From Eq. (4) it follows, that

as it is for the perfect gas.
But some other properties of a real gas at p → 0 differ from that of the perfect gas. For example, from Eq. (4)

Since  , the molar volume of a perfect gas, and taking into consideration Eq. (5), from Eq. (7) it follows
, the molar volume of a perfect gas, and taking into consideration Eq. (5), from Eq. (7) it follows

from which

The same is valid, for instance, for the Joule-Thomson coefficient α

where  denotes the molar enthalpy and
denotes the molar enthalpy and  molar heat capacity.
molar heat capacity.
From the thermodynamic differential equation:

It follows that for a perfect gas  and α = 0.
and α = 0.
But for a real gas at p → 0

which in general is not zero and therefore  .
In thermodynamic and thermochemical calculations, the so-called perfect gas thermodynamic functions are used:
.
In thermodynamic and thermochemical calculations, the so-called perfect gas thermodynamic functions are used:  (molar Helmholtz energy);
(molar Helmholtz energy);  (molar Gibbs energy). For a real gas the respective functions are equal to the perfect gas functions at p → 0.
(molar Gibbs energy). For a real gas the respective functions are equal to the perfect gas functions at p → 0.