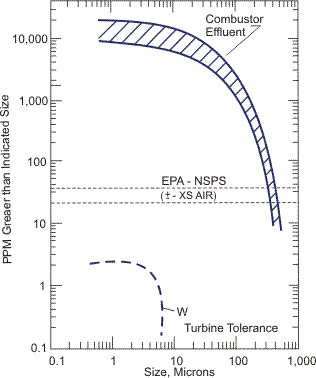
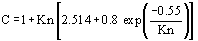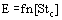Particulate solids are separated from gas streams for a variety of reasons. In some instances, the interest is in the recovery of solids as a product, e.g., following a milling operation for which a combined classification and separation is often required [Prasher ( 1987)]. In other cases, the emission of fine particulate solids and dust from a unit operation may be excessive and, therefore, a reduction and control of particulate level is required for the protection of subsequent process equipment or for the environmental emission [Strauss (1975, and Theodore and Buonicore (1976)]. This is illustrated in Figure 1 for the case of advanced power generation from coal, where it is desirable to expand the hot gases in a gas turbine before exhaust to atmosphere to enhance the efficiency of power generation. Typical particulate effluent from a pilot-scale fluidized bed combustor is shown, together with upper limits of allowable emission to atmosphere, and of the inlet dust tolerance of high performance gas turbines [Henry et al. (1982)]. In this section, an overview of the principles of gas-solids separation is given. Details of various technologies are addressed in the next three sections.
The most commonly used techniques for the separation of particulate solids from gases are inertial separators, Electrostatic Separators and Filters. The physical phenomena involved in the separation of solids from gases are influenced by a number of important factors such as the properties of the gas, and gas-particle and particle-particle interactions. These factors are briefly reviewed here first before addressing the principles of various types of gas-solids separators.
Over the range of pressures commonly used in industrial gas-solids separation processes, departures from ideal gas behavior are negligible. Therefore the density of a gas at pressure P and absolute temperature T can be approximated by

where Mw is the mean molecular weight of the gas,  the molar volume, and
the molar volume, and  the universal gas constant.
the universal gas constant.
Elementary kinetic theory gives a first approximation for the effect of temperature and pressure on gas viscosity. Viscosity is predicted to be independent of pressure, and proportional to the square root of absolute temperature.
In addition to these macroscopic properties, the Mean Free Path of gas molecules, λ, is of interest for removal of fine particles. Elementary kinetic theory predicts that λ is inversely proportional to density, so that

Almost any particle removal process requires the particles to migrate relative to the gas, so that the drag of the gas on the particle is of prime interest. The particle Reynolds Number is defined as

where dp is the particle diameter and u the velocity of the particle relative to the gas and η the gas viscosity. In most applications, Rep remains small. The drag force, FD, can then be estimated from Stokes' Law with a correction to allow for "slip effects" which arise when the particle diameter is comparable to the mean free path of gas molecules:
where C is the slip correction factor or "Cunningham coefficient" defined as

C can be estimated empirically from Davies' correlation (1945):
where Kn is the Knudsen Number:

Equation (6) is applicable to spherical particles, and Beard (1976), and Gift et al., (1978) summarize modifications for nonspherical particles. Some representative values for C are given by Clift et al., (1981). It is worth noting that, whereas C only departs significantly from unity for submicron particles at ambient conditions and at elevated pressure, slip effects are significant for particles several microns in diameter at elevated temperatures and ambient pressure.
For Reynolds numbers larger than, say, 0.1, Equation (4) is better replaced by the general form:
where CD is an empirical function of Rep Of the many forms suggested for CD (Rep), that due to Schiller and Nauman (1933) is probably most accurate for Rep < 800:

When ReP is sufficiently large that Equation (8) must be used rather than Eq. (4), then slip effects can be ignored, unless u is significant by comparison with the speed of sound in the gas. However, this is not normally the case in industrial gas-solids separation processes.
For a particle settling freely under its own weight in a gas, the drag force counterbalances the immersed weight of the particle. For low Rep, terminal velocity then follows from Equation (4) as

where ρp is the particle density. Normally ρp≥ρg , so that Eq. (1) can be written

Increasing temperature, through its effect on gas viscosity, increases fluid-particle drag, reduces settling velocity, and generally makes removal of particles from gases more difficult. The effect of pressure is smaller, and acts through the slip effect so that it is only significant for particles typically smaller than about 1 μm; in general, the effect of increasing pressure is again to make particle removal more difficult. Electrostatic precipitators can be an exception to this rule because of the effect of pressure on the electrical properties of a gas. Increasing the pressure, within the range of interest here, widens the gap between the corona-starting and sparkover voltages. Therefore, the effect of increased drag on the particle at high pressure and high temperature may be compensated or even overcome by increasing the electrostatic field intensity (see below).
In certain types of filter the Brownian diffusivity of particles in the gas is of concern. This is usually best evaluated by the Stokes-Einstein equation [Clift et al. (1981)]:

where kB is Boltzmann's constant, 1.380622×10−23 JK−1. Taking the effect of temperature on viscosity into account, for given particle size

so that the Brownian diffusivity increases with increasing temperature. Pressure has a weaker effect, through the slip correction factor, C, increasing pressure decreases DAB It follows from the above that, if the efficiency of a gas-solids separation process is to be investigated, it is more important to match the process temperature than pressure. Pressure is important for fine particles, so that devices such as electrostatic precipitators intended to collect micron-sized particles would be tested at process temperature and pressure; electrical properties also dictate that both pressure and temperature should be matched.
In some devices for particle collection, most notably electrostatic precipitators and some types of filter, it is essential for the collected particles to form relatively large agglomerates which can then be removed easily. Particle-particle cohesive forces arising from electrostatic, van der Waals and capillary effects are then important.
Electrostatic effects act over the longest range and may therefore be effective in separating particles from gases. However, they can only contribute to the cohesiveness of a deposited particulate if the constituent particles carry both positive and negative charges. Corny and Clift (1984) have shown that fly-ash from fluidized combustion can carry such charges, and be highly cohesive as a result. However, it is not known whether this phenomenon occurs more generally nor, for example, whether ash which has been raised above the fusion temperature carries significant charges. More generally, particles are likely to carry charges of the same sign, so that interparticle Coulombic repulsion acts against cohesion. Leakage of this charge requires a conductive path to an earthed surface, and this depends in particular on the surface characteristics of the particles. If the particles have for some reasons low surface resistivity, then electrical contact between particles can be good and the charge can leak away relatively rapidly. This is particularly important in electrostatic precipitation.
The other two types of force act over shorter ranges, and thefore represent genuine cohesion. Whereas electrostatic forces result from overall surplus of deficit of electrons, van der Waals forces arise from the attraction between atomic or molecular dipoles. Because they result from processes occurring on a molecular scale, van der Waals forces act over much shorter ranges than electrostatic forces. The strength of van der Waals cohesion depends on the value of the Hamaker constant, a characteristic property of the material comprising the particles. The Hamaker constant is effectively independent of pressure, and the dependence on temperature is not well understood but is probably weak. Hence the environment affects van der Waals cohesion mainly through its effect on surface properties. Dahneke (1972) showed that local deformation of the contacting surfaces can increase substantially the strength of interparticle cohesion.
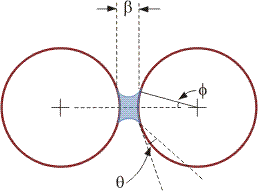
Capillary forces, which result from a liquid film on the surface of the particles, are orders of magnitude stronger than van der Waals forces (see also Capillary Action). Figure 2 shows schematically a "pendular bridge" between two idealized particles of diameter dp For zero particle separation (β = 0) and a fully-wetting liquid (contact angle, θ = 0) the attractive force between the particles is [Fisher (1926)]:
where  is the angle defining the size of the bridge and σ is the tension at the gas/liquid interface. According to Equation 12, the cohesive force increases as the liquid bridge becomes smaller, to a limiting value for
is the angle defining the size of the bridge and σ is the tension at the gas/liquid interface. According to Equation 12, the cohesive force increases as the liquid bridge becomes smaller, to a limiting value for  of πdσ. This theoretical result is not applicable to real particles with rough surface [Cheng (1970)]; for particles which contact at points of asperity the cohesive force increases with liquid film thickness [Coughlin et al. (1982)].
of πdσ. This theoretical result is not applicable to real particles with rough surface [Cheng (1970)]; for particles which contact at points of asperity the cohesive force increases with liquid film thickness [Coughlin et al. (1982)].
Inertial Separators cover devices in which the main property used in recovering particles is their density, so that they are removed by centrifugal action. Deliberate changes in the direction of gas flow causes the particles trajectories to deviate from the gas streamlines, thus concentrating and separating the particles from the gas. Inertial separators are varied in design. Most separators in this category use passive mechanical separation with induced centrifugal motion, such as cyclones. There are however separators in which the centrifugal motion is induced by a rotating propeller. These devices are often used for classification purposes, and are covered in Classifiers.
Inertial separators can be used in a wide range of pressure and temperature conditions. Their performance is satisfactory for coarse particles, but as the particle size decreases much below 10 μm the collection efficiency deteriorates very rapidly. Of the various types of design, the reverse flow cyclone with tangential entry is the most common type of inertial separators due to its compactness, simplicity of construction and operation, and high throughput. The inlet can be made either truly tangential or wrapped around the body, commonly referred to as "tangential entry" and "volute entry" or "scroll inlet", respectively. The former has a higher collection efficiency, but at the expense of higher pressure drop. There are, of course, other designs using axial entry with vanes installed within the cyclone to induce rotation, direct through-flow of gas without reversing, and blowdown, where a small fraction of the gas is allowed to flow with the collected solids [Strauss (1975)].
Performance analysis of cyclones has been approached on both phenomenlogical as well mechanistic levels. On a phenomenological level, conventional dimensional analysis leads to the definition of groups which can be used to "scale" cyclone performance for effects of size, throughput and process conditions, see Abrahamson (1981). The collection efficiency, E, for particles of diameter dp and density ρp from a gas of density ρg and viscosity η is given by a relationship of the form

while the pressure drop across the cyclone, ΔP, follows a relationship with the general form

In Eqs. (13) and (14),  is the volumetric flowrate of gas through the cyclone, and D is the cyclone barrel diameter. Therefore
is the volumetric flowrate of gas through the cyclone, and D is the cyclone barrel diameter. Therefore  represents a characteristic gas velocity, such as the mean inlet gas velocity, as the inlet dimensions are fixed relative to the barrel diameter for a given design. The two independent dimensionless groups in Eq. (13) can be regarded as the cyclone Stokes number, Stc, and Reynolds number, Rec
represents a characteristic gas velocity, such as the mean inlet gas velocity, as the inlet dimensions are fixed relative to the barrel diameter for a given design. The two independent dimensionless groups in Eq. (13) can be regarded as the cyclone Stokes number, Stc, and Reynolds number, Rec


The Stokes number describes the tendency of the particle trajectories to deviate from gas streamlines, and the Reynolds number describes the gas flow condition within the cyclone. The above analysis is only valid for low particle concentrations, where the probability of collection of any individual particle is unaffected by other particles present. For industrial cyclones, the gas flow in the cyclone is turbulent and Rec is very large. It is therefore commonly assumed that the collection efficiency is not affected by the gas flow pattern, and the effect of Rec is neglected. This leads to the commonly used scaling laws, see, for example, Strauss (1975):
Equations (17) and (18) have been shown to work well for low particle loadings and for particles carrying low levels of electric charge [Giles (1982)]. However, for the cases where particle/particle interactions are significant, including electrical effects, the above correlations are not satisfactory and E is less sensitive to Stc
The effect of temperature and pressure is in principle reflected in the density and viscosity of the gas. However, care must be taken in the use of Equation (17) in this case because temperature and pressure can also modify Rec, which it can then alter the flow condition, thus producing an effect which is not taken into account in Equation (17).
The alternative approach to analysis of cyclone performance is by mechanistic modelling, which is necessary to account for the effect of pressure and temperature, as well as for predicting the effects of changing cyclone geometry. Clift et al. (1991) have recently reviewed a number of widely used models of cyclones, i.e., those due to Leith and Licht (1972), Muschelknautz (1970), Dietz (1981) and Mothes and Löffler (1988). It emerges from their analysis that the models of Dietz (1981) and Mothes and Löffler (1988) provide the best agreement with a very wide range of experimental data reported in the literature.
Electrostatic Separators cover devices in which the main separating effect is migration of electrically charged particles in an imposed electric field. These devices have a high collection efficiency for a wide range of particle sizes, and are particularly suitable for submicrometer solids. They have at the same time a high throughput and low pressure drop, which are the main attributes for their wide use in the power generation industry. Operation under extreme conditions of temperature (i.e., above about 800°C) is difficult unless it is accompanied by high pressures, as it will be described below. Apart from the problems of integrity of materials of containment and construction, further considerations limit operation at elevated temperature and pressure. Insulating materials are required to prevent excessive current leakage between the electrodes. Breakdown of the gas between the electrodes must also be avoided. The minimum potential gradient causing ionic breakdown of a gas generally decreases with increasing temperature but increases with pressure. Therefore, at elevated temperature, there is generally a minimum pressure, dependent on gas composition, below which a precipitator cannot be operated. The electric properties of the particulate are also relevant: if it is highly resistive, then collected dust retains its charge and reduces the efficiency of collection of further particulates. It is also necessary for the collected dust to be removed from the precipitating electrode. This is normally achieved intermittently by some mechanical action such as "rapping" and the detached particles are allowed to settle to the base of the equipment. For this to be possible, the dust must detach as agglomerates with high terminal settling velocity; thus some cohesiveness of the collected dust is necessary to avoid excessive re-entrainment on electrode cleaning.
The process of electrostatic precipitation involves three stages:
charging of suspended particles by corona discharge;
migration and deposition of the charged particles under the influence of an applied electrostatic field;
removal of the collected material from the collecting electrode and transfer to a suitable receptacle outside the precipitator.
In industrial-scale electrostatic precipitation, stages (a) and (b) are generally combined and the electrostatic field also produces the necessary corona discharge for particle charging. The principles of operation are described by Strauss (1975) and by Böhm (1982). It is important to establish a stable corona having adequate current to provide complete charging of the particles, without getting sparkovers. The onsets of corona voltage and sparkover voltage depend on the geometry of the electrodes, type of gas and the operating temperature and pressure. The corona-starting voltage increases slowly as the pressure is increased, for both positive and negative corona. The effect of pressure on sparkover voltage is more prominent. The sparkover voltage increases rapidly as the pressure is increased above atmospheric, but reaches a maximum and declines, to coincide eventually with the corona-starting voltage, see Robinson (1971). The pressure at which the corona-starting and sparkover voltages coincide is called the "critical pressure". The interaction of two opposing effects is considered responsible for the existence of the critical pressure point as the pressure is raised (at constant temperature).
shorter mean-free paths impede ionization by collision, and so tend to raise the sparkover level;
enhanced photoionization and reduced ion diffusion tend to facilitate streamer propagation from the anode across the gas.
As the pressure increases, the initially dominant first effect gives way to the second, the streamer develops across the gas, and at the critical pressure, spark breakdown ensues.
The effect of temperature has been studied by various authors and the results of the earlier work have been summarized by Robinson (1971). Briefly, the earlier works indicated that, for temperatures up to about 1073 K (800°C), the current-voltage relations for positive corona were a function of relative gas density only, but for negative corona the density and temperature had independent influences for temperatures above 823 K (550°C). At temperatures higher than 800°C, thermal ionization was considered to become high enough to play a significant role and eventually lead to breakdown. In this case a positive corona was predicted to be required for most types of gases, as the space charge produced by thermal ionization would generally be positive due to sweeping out of highly mobile electrons.
In more recent years, Bush et al. (1977 and 1979) investigated the range of temperature and pressure in which stable corona discharge may be obtained, and established current-voltage characteristics in a particle-free electrostatic precipitator for dry air, a simulated combustion gas and a substitute fuel gas at temperatures up to 1366K (1093°C) and pressures up to 35.5 bar. Their results show that excessive current and sparkover due to thermal ionization, anticipated previously, are not encountered within the range tested. The results also reveal the tendency for the positive sparkover voltage to exceed that of the negative sparkover for temperatures above 533 K and low relative air densities (below about 2), a trend which had been observed by earlier workers. However, experience with dust-laden gases has consistently shown that positive coronas are inherently less stable than negative, and also yield a lower collection efficiency due to lower corona currents.
The results of Bush et al. show that the critical pressure increases with temperature. The critical pressure for negative corona discharge is much higher than for positive. It is worth noting that, due to the increase of critical pressures with temperature, the range of pressure for stable corona becomes wider at high temperatures. Thus precipitation could be made more efficient by applying higher voltages as temperature and pressure increase together. However, these conclusions are based on dust-free gases, and the performance evaluations reported so far cannot confirm with confidence their extension to dust-laden gases.
The bulk of the particles passing through the charging zone acquire electric charges of the same polarity as the discharge electrode; i.e., negative for negative corona. Two distinct mechanisms are involved in the charging process:
Field charging, caused by bombardment of the particles by ions migrating under the influence of the overall electric field.
Diffusion charging, resulting from attachment to the particles of ions which contact them in the course of their random movement through the gas.
Field charging is the dominating mechanism for large particles, typically greater than 1.0 μm. Its rate depends on the field intensity as well as on ion concentration. Diffusion charging is dominant for very fine particles, smaller than 0.1 μm. In industrial precipitators the particle residence time in the charging zone is large, and the particles reach their saturation charge level, which may be estimated from Equation (19) due to Cochet (1956 and 1961). This equation includes the effect of diffusion charging in the field charging process, hence taking into account both mechanisms
where q is the charge acquired by a particle of diameter dp in the field of strength E0, kp is the relative dielectric constant of the particle, ε0 is the permittivity of free space, and λ is the gas mean free path.
Under the influence of the electric field, charged particles migrate towards the collecting electrode. The migration velocity, ω, is commonly calculated from the quasi-steady force balance between Stokes' drag and the applied electrostatic force:

where Ep is the precipitating electric field. Hence,

where C is the slip correction factor. In practice, ω is determined empirically because of various complicating factors such as the presence of particle size and shape distributions, turbulence and ionic wind.
The collection efficiency of an electrostatic precipitator is related to the migration velocity by the celebrated Deutsch (1922) model. Details of this model and other technological issues such as the grade efficiency and particle collection and discharge are given in the section on the electrostatic precipitators.
Filters cover all devices in which the gas to be cleaned passes through a porous or permeable medium which collects and retains particles carried by the gas. In a membrane-type filler, the passages through the medium are comparable to or smaller than the particulate. Filtration then occurs by mechanical obstruction, and the particulate builds up as a filter "cake" on the upstream face of the filter. The filtration efficiency is essentially absolute, and virtually all the dust is retained on the upstream surface of the filter. In other types of filter, such as granular bed or fibre filters, the passages through the medium are typically large compared to the particulate to be collected. The particulate is therefore collected initially within the bed by the individual granules or fibres. This process is called depth filtration, and it continues until the passages on the upstream side of the filter narrow down, leading to bridging over the openings where a cake starts to form. In the initial stage of filtration here, the efficiency of the filter mid retention of the particulate by the medium is of concern, while in the later stage of filtration, where a cake has formed, the efficiency is high and the increase in the pressure drop across the filter is of concern as in the membrane-type filters.
Filters require regular cleaning as the level of dust builds up on the filter. Various methods of cleaning are used depending on the filter type. Membrane filters are sometimes used just once and are then replaced or they are cleaned in situ by some intermittent mechanical process such as vibration or reverse pressure pulse or reverse gas flow rate. A similar cleaning process is applied to those filters which may operate initially by depth filtration, but rely on cake formation as the main filtration mechanism. The granular type filters, on the other hand, employ beds of unbounded filter elements, which are. usually removed continuously or intermittently for regeneration of the filter medium. In some cases, the elements are cleaned in situ, as for a membrane filter.
The range of materials used as filter medium is very wide indeed; it includes natural and man-made fibres, and porous sintered polymer, metal and ceramic sheets and tubes. The main filter medium requirements are:
durability of the medium at process conditions;
the ability of the dust to form a cake on the medium;
filter performance during the initial stage of cake formation following cleaning;
ability of the medium to withstand mechanical stresses during cleaning;
form of cake detached during cleaning;
"blinding" of the filter medium either by depth filtration or by permanent adhesion of cake to medium.
Appropriate choice of filter medium depends on the process conditions and type of dust material. High temperature applications impose a great constraint on the choice of filter medium. Recent developments in this field have been addressed in a symposium on gas cleaning at high temperatures [see Clift and Seville (1993)].
The process of filtration is analyzed in terms of three fundamental aspects of primary collection of dust from the gas, retention or rebound of dust from the collector, and the effect of collected dust on the filter structure.
For primary collection, the important mechanisms in general are: (i) deposition by diffusion; (ii) gravitational settling; (iii) inertial deposition; (iv) direct interception; (v) electrostatic deposition. Magnetic and thermal deposition may also occur depending on the application. The collection efficiency of each individual mechanism is conventionally presented in terms of single fibre or granule collection efficiency, E, defined by

with E a function of dust and granule or fibre size and charge, dust density, gas properties, and bed voidage. For a particular dust size in a given filter, the penetration is defined as:

The single particle collection efficiency depends on type and structure of filter medium. Furthermore, its relationship with the penetration is established through mathematical modelling of filtration process. For granular type filters, the single particle collection efficiency of the first four mechanical collection mechanisms has been summarized by Ghadiri et al. (1993). The electrical deposition mechanism is given by Coury (1983), and the magnetic collection by Birss and Parker (1981). For depth filters using fabric medium, various correlations for E have been summarized by Strauss (1975) and Löffler (1971). For granular bed filters, the relationship between E and f has been outlined by Ghadiri et al. (1993) and by Clift et al. (1981). Applications to fluidised bed filters at elevated temperatures have been discussed by Ghadiri et al. (1986). For fabric filters, the relationship between E and f has been analyzed by Schweers and Löffler (1994), taking account of the distribution of inter-fibre spacings.
When a dust particle makes contact with a filter element, it is essential that it is retained rather than rebounding, as it may lead to the re-entrainment of the particle. Retention is dominated by short-range adhesive forces. The analysis of retention was initiated by Dahneke (1971), and developed further by Stenhouse and Freshwater (1976), Hiller and Löffler (1978), Clift (1983) and more recently by Ning (1995). The approach is based on an energy balance between the kinetic energy of the approaching particle, Ei, and the detachment energy, Ed In addition to Ei, the particle acquires further energy in approaching the collector due to the very short van der Waals forces, Ev The energy at the instant of rebound is then e2(Ei + Ev), where e is the coefficient of restitution; the kinetic energy lost is due to the dispersion of elastic waves as well as plastic deformation of the particle or the collector. In order to detach from the surface, the particle energy must exceed the detachment energy, Ed Thus the particle adheres if

The above inequality indicates a critical impact velocity above which a particle will rebound from the filter element. The detachment energy Ed is the sum of energies due to van der Waals forces, and electrostatic and capillary attractions if they are present. Plastic deformation enhances cohesion because of the larger contact area than otherwise possible with elastic deformation alone, and this has recently been modelled by Ning (1995).
Cake formation is essential in those filter types whose medium has large passages and the initial stage of filtration is by depth filtration. Interparticle cohesion is essential for cake formation to occur. The process starts with particle chain formation, leading to arching over the openings of the filter, hence providing the foundation for build up of a cake. If the interparticle cohesion is low or the span of the passages is too wide, the arch may be weak and it may fail under stresses due to the pressure drop in the cake. In this case, the dust particles will break into the filter, i.e., pinhole formation, which causes long-term "blinding" of the filter. Ghadiri et al. (1989) showed that pinhole formation can be reduced by electrical enhancement of the interparticle cohesion. Coury (1983) has shown that particles that carry substantial electrical charges of both signs, such as fly-ash, readily form a cake, where uncharged and uncohesive particles, such as coal char, fail to form a cake under otherwise identical conditions. Cake formation is therefore strongly influenced by interparticle forces including van der Waals, electrostatic and capillary forces.
Filter cleaning is another important aspect of filter operation. It should be carried out in such a way that the cake is detached completely from the filter, i.e., without leaving patches of particles still adhering to the filter. At the same time, the cake coherence should be preserved so that the particles are not redispersed in the gas stream. Current practice in filter cleaning is largely empirical. However, much of recent work has centered on developing an understanding of the mechanisms involved from which some operational guidelines have emerged [see Cliff and Seville (1993)].
REFERENCES
Abrahamson, J. (1981) Progress in Filtration and Separation, Vol. 2, Ed. R. J. Wakeman, Elsevier, Amsterdam, pp. 1-74.
Beard, K. V. (1976), Terminal Velocity and Shape of Cloud and Precipitation Drops Aloft, J. Atmos. Sci., 33, pp. 851-864. DOI: 10.1175/1520-0469(1976)033<0851:TVASOC>2.0.CO;2
Birss, R. R. and Parker, M. R. (1981) High Intensity Magnetic Separation, in Progress in Filtration and Separation, Vol. 2, Ed. R. J. Wakeman, Eisevier, Amsterdam, pp. 171-303.
Böhm, J. (1982) Electrostatic Precipitators, Elsevier, Amsterdam.
Bush, J. R., Feldman, P. L. and Robinson, M. (1977) Development of a High-Temperature/High Pressure Electrostatic Precipitator, EPA-600/7-77-132.
Bush, J. R., Feldman, P. L. and Robinson, M. (1979) High Temperature High Pressure Electrostatic Precipitation, Air Pollution Control Ass. 29, pp. 365-371
Cheng, D. C. H. (1970) J. Adhesion, 2, 82.
Clift, R. (1983) Trans. Inst. Engrs. Aust. ME8, 181.
Gift, R., Grace, J. R. and Weber, M. E. (1978) Bubbles, Drops and Particles, Academic Press, New York.
Clift, R., Ghadiri, M. and Thambimuthu, K. V. (1981) in Progress in Filtration and Separation, Vol. 2, Ed. R. J. Wakeman, Elsevier, Amsterdam, pp. 75-124.
Clift, R., Ghadiri, M. and Hoffman, A. C. (1991), A critique of two models for cyclone performance, A.I.Ch.E.J. 37(2), pp. 285-289.
Clift, R. and Seville, J. P. K. (1993)Gas Cleaning at High Temperatures, Blackie Academic and Professional, London.
Cochet, R. (1956), Théorie de la charge des particules submicronique, Compt. Rend. 243, 243.
Cochet, R. (1961) Colloq. Inter. Centre Nat. Rech. Sci. (Paris), 102, 331.
Coughlin, R. W., Elbirli, B. and Vergara-Edwards, L. (1982), Interparticle force by capillary-condensed liquid at contact points, J. Colloid and Interface Sci. 87, 18. DOI: 10.1016/0021-9797(82)90368-X
Coury, J. R. (1983) Ph.D. Dissertation, University of Cambridge.
Coury, J. R. and Clift, R. (1984) in Electrical and Magnetic Separation and Filtration Technology, Koninklijke Vlaamse Ingenieurvereniging, Antwerp, p. 27.
Dahneke, B. (1971), The capture of aerosol particles by surfaces, J. Colloid and Interface Sci. 37, 342. DOI: 10.1016/0021-9797(71)90302-X
Dahneke (1972), The influence of flattening on the adhesion of particles, J. Colloid and Interface Sci. 40, 1. DOI: 10.1016/0021-9797(72)90168-3
Davies, C. N. (1945) Proc. Phys. Sci. 57, 259.
Deutsch, W. (1922) Ann. Physik, 68, 335.
Dietz, P. W. (1981)Collection Efficiency of Cyclone Separators, A.ICh.E.J. 27, pp. 888-892.
Fisher, R. A. (1926) J. Agric. Soc. 16, 492.
Ghadiri, M., Cleaver, J. A. S. and Seaton, R. (1989) Electrically Enhanced Gas Filtration Using Microsieves as Filter Media (1989) 1st European Symposium on Separation of Particles from Gases, PARTEC, Nuremberg, 19-21 April 1989.
Ghadiri, M., Seville, J. P. K. and Clift, R. (1986) The Use of Fluidised Beds to Filter Gases at High Temperatures, I. Chem. E. Symp. Series No. 99, pp. 351-361.
Ghadiri, M., Seville, J. P. K. and Clift, R. (1993) Fluidised Bed Filtration of Gases at High Temperatures, Trans. I. Chem. E. 71, Part A, pp. 371 -381.
Giles, W. B. (1982) Cyclone Scaling Experiments, 4th Symp. on the Transfer and Utilisation of Particulate Control Technology, 11-15 Oct. 1982, Houston, USA.
Henry, R. F., Saxena, S. C. and Podolski, W. F. (1982) Particulate Removal from High-Temperature, High-Pressure Combustion Gases, Argonne National Laboratory Report, ANL/FE-82-11.
Hiller, R. and Löffler, F. (1978) Deposition and Filtration of Particles from Gases and Liquids, SCI, London, p. 81.
Leith, D. and Licht, W. (1972) The Collection Efficiency of Cyclone Type Particle Collectors—a New Theoretical Approach, A.I.Ch.E. Symp.Ser. 68 (126), pp. 196-206.
Löffler, F. (1971) Collection of Particles by Fibre Filters in Air Pollution Control, Part I, W. Strauss, Ed. Wiley-Intersciences, pp. 337-375.
Mothes, H. and, F. (1988) Prediction of Particle Removal in Cyclone Separators, Int. Chem. Eng. 28 (2), pp. 231-240.
Muschelknautz, E. (1970) Design of Cyclone Separators in the Engineering Practice, Staub-Reinhalt. Luft, 30 (5) pp. 1-12.
Ning, Z. (1995) Ph.D. Dissertation, Aston University, Birmingham.
Prasher, C. L. (1987) Crushing and Grinding Process Handbook, Wiley, Chichester.
Robinson, M. (1971) Electrostatic Precipitation in Air Pollution Control, Part I, W. Strauss, Ed., Wiley-Intersciences.
Schiller, L. and Nauman, A. Z. (1933), Uber die grundlegenden Berechnungen bei der Schwerkraftaufbereitung, Ver: Deut. Ing. 77, pp. 310-320.
Schweers, E and Löffler, F. (1994) Realistic Modelling of the Behaviour of Fibrous Filters through Consideration of Filter Structure, Powder Technology, 80 (3), pp. 191-206. DOI: 10.1016/0032-5910(94)02850-8
Stenhouse, J. I. T. and Freshwater, D. C. (1976) Trans. I. Chem. E. 54, 95.
Strauss, W. (1975) Industrial Gas Cleaning, 2nd edn. Pergamon Press, Oxford.
Theodore, L. and Buonicore, A. J. (1976) Industrial Air Pollution Control Equipment for Particulates, CRC Press, Cleveland, Ohio.
参考文献列表
- Abrahamson, J. (1981) Progress in Filtration and Separation, Vol. 2, Ed. R. J. Wakeman, Elsevier, Amsterdam, pp. 1-74.
- Beard, K. V. (1976), Terminal Velocity and Shape of Cloud and Precipitation Drops Aloft, J. Atmos. Sci., 33, pp. 851-864. DOI: 10.1175/1520-0469(1976)033<0851:TVASOC>2.0.CO;2
- Birss, R. R. and Parker, M. R. (1981) High Intensity Magnetic Separation, in Progress in Filtration and Separation, Vol. 2, Ed. R. J. Wakeman, Eisevier, Amsterdam, pp. 171-303.
- Böhm, J. (1982) Electrostatic Precipitators, Elsevier, Amsterdam.
- Bush, J. R., Feldman, P. L. and Robinson, M. (1977) Development of a High-Temperature/High Pressure Electrostatic Precipitator, EPA-600/7-77-132.
- Bush, J. R., Feldman, P. L. and Robinson, M. (1979) High Temperature High Pressure Electrostatic Precipitation, Air Pollution Control Ass. 29, pp. 365-371
- Cheng, D. C. H. (1970) J. Adhesion, 2, 82.
- Clift, R. (1983) Trans. Inst. Engrs. Aust. ME8, 181.
- Gift, R., Grace, J. R. and Weber, M. E. (1978) Bubbles, Drops and Particles, Academic Press, New York.
- Clift, R., Ghadiri, M. and Thambimuthu, K. V. (1981) in Progress in Filtration and Separation, Vol. 2, Ed. R. J. Wakeman, Elsevier, Amsterdam, pp. 75-124.
- Clift, R., Ghadiri, M. and Hoffman, A. C. (1991), A critique of two models for cyclone performance, A.I.Ch.E.J. 37(2), pp. 285-289. DOI: 10.1002/aic.690370217
- Clift, R. and Seville, J. P. K. (1993)Gas Cleaning at High Temperatures, Blackie Academic and Professional, London.
- Cochet, R. (1956), Théorie de la charge des particules submicronique, Compt. Rend. 243, 243.
- Cochet, R. (1961) Colloq. Inter. Centre Nat. Rech. Sci. (Paris), 102, 331.
- Coughlin, R. W., Elbirli, B. and Vergara-Edwards, L. (1982), Interparticle force by capillary-condensed liquid at contact points, J. Colloid and Interface Sci. 87, 18. DOI: 10.1016/0021-9797(82)90368-X
- Coury, J. R. (1983) Ph.D. Dissertation, University of Cambridge.
- Coury, J. R. and Clift, R. (1984) in Electrical and Magnetic Separation and Filtration Technology, Koninklijke Vlaamse Ingenieurvereniging, Antwerp, p. 27.
- Dahneke, B. (1971), The capture of aerosol particles by surfaces, J. Colloid and Interface Sci. 37, 342. DOI: 10.1016/0021-9797(71)90302-X
- Dahneke (1972), The influence of flattening on the adhesion of particles, J. Colloid and Interface Sci. 40, 1. DOI: 10.1016/0021-9797(72)90168-3
- Davies, C. N. (1945) Proc. Phys. Sci. 57, 259.
- Deutsch, W. (1922) Ann. Physik, 68, 335.
- Dietz, P. W. (1981)Collection Efficiency of Cyclone Separators, A.ICh.E.J. 27, pp. 888-892. DOI: 10.1002/aic.690270603
- Fisher, R. A. (1926) J. Agric. Soc. 16, 492.
- Ghadiri, M., Cleaver, J. A. S. and Seaton, R. (1989) Electrically Enhanced Gas Filtration Using Microsieves as Filter Media (1989) 1st European Symposium on Separation of Particles from Gases, PARTEC, Nuremberg, 19-21 April 1989.
- Ghadiri, M., Seville, J. P. K. and Clift, R. (1986) The Use of Fluidised Beds to Filter Gases at High Temperatures, I. Chem. E. Symp. Series No. 99, pp. 351-361.
- Ghadiri, M., Seville, J. P. K. and Clift, R. (1993) Fluidised Bed Filtration of Gases at High Temperatures, Trans. I. Chem. E. 71, Part A, pp. 371 -381.
- Giles, W. B. (1982) Cyclone Scaling Experiments, 4th Symp. on the Transfer and Utilisation of Particulate Control Technology, 11-15 Oct. 1982, Houston, USA.
- Henry, R. F., Saxena, S. C. and Podolski, W. F. (1982) Particulate Removal from High-Temperature, High-Pressure Combustion Gases, Argonne National Laboratory Report, ANL/FE-82-11.
- Hiller, R. and Löffler, F. (1978) Deposition and Filtration of Particles from Gases and Liquids, SCI, London, p. 81.
- Leith, D. and Licht, W. (1972) The Collection Efficiency of Cyclone Type Particle Collectors—a New Theoretical Approach, A.I.Ch.E. Symp.Ser. 68 (126), pp. 196-206.
- Löffler, F. (1971) Collection of Particles by Fibre Filters in Air Pollution Control, Part I, W. Strauss, Ed. Wiley-Intersciences, pp. 337-375.
- Mothes, H. and, F. (1988) Prediction of Particle Removal in Cyclone Separators, Int. Chem. Eng. 28 (2), pp. 231-240.
- Muschelknautz, E. (1970) Design of Cyclone Separators in the Engineering Practice, Staub-Reinhalt. Luft, 30 (5) pp. 1-12.
- Ning, Z. (1995) Ph.D. Dissertation, Aston University, Birmingham.
- Prasher, C. L. (1987) Crushing and Grinding Process Handbook, Wiley, Chichester.
- Robinson, M. (1971) Electrostatic Precipitation in Air Pollution Control, Part I, W. Strauss, Ed., Wiley-Intersciences.
- Schiller, L. and Nauman, A. Z. (1933), Uber die grundlegenden Berechnungen bei der Schwerkraftaufbereitung, Ver: Deut. Ing. 77, pp. 310-320.
- Schweers, E and Löffler, F. (1994) Realistic Modelling of the Behaviour of Fibrous Filters through Consideration of Filter Structure, Powder Technology, 80 (3), pp. 191-206. DOI: 10.1016/0032-5910(94)02850-8
- Stenhouse, J. I. T. and Freshwater, D. C. (1976) Trans. I. Chem. E. 54, 95.
- Strauss, W. (1975) Industrial Gas Cleaning, 2nd edn. Pergamon Press, Oxford.
- Theodore, L. and Buonicore, A. J. (1976) Industrial Air Pollution Control Equipment for Particulates, CRC Press, Cleveland, Ohio.